d.addPairwiseGaussian(sxy=20, compat=3)
    d.addPairwiseBilateral(sxy=30, srgb=20, rgbim=img, compat=10)

pairwise_energy = create_pairwise_bilateral(sdims=(10,10), schan=(0.01,), img=img, chdim=2)
d.addPairwiseEnergy(pairwise_energy, compat=10)  # `compat` is the "strength" of this potential.

import pydensecrf.densecrf as dcrf
from pydensecrf.utils import unary_from_softmax, create_pairwise_bilateral

import numpy as np
import matplotlib.pyplot as plt

from scipy.stats import multivariate_normal

plt.rcParams['image.interpolation'] = 'nearest'
plt.rcParams['image.cmap'] = 'gray'


H, W, NLABELS = 400, 512, 2

# This creates a gaussian blob...
pos = np.stack(np.mgrid[0:H, 0:W], axis=2)
rv = multivariate_normal([H//2, W//2], (H//4)*(W//4))
probs = rv.pdf(pos)

# ...which we project into the range [0.4, 0.6]
probs = (probs-probs.min()) / (probs.max()-probs.min())
probs = 0.5 + 0.2 * (probs-0.5)

# The first dimension needs to be equal to the number of classes.
# Let's have one "foreground" and one "background" class.
# So replicate the gaussian blob but invert it to create the probability
# of the "background" class to be the opposite of "foreground".
probs = np.tile(probs[np.newaxis,:,:],(2,1,1))
probs[1,:,:] = 1 - probs[0,:,:]

# Let's have a look:
plt.figure(figsize=(15,5))
plt.subplot(1,2,1); plt.imshow(probs[0,:,:]); plt.title('Foreground probability'); plt.axis('off'); plt.colorbar();
plt.subplot(1,2,2); plt.imshow(probs[1,:,:]); plt.title('Background probability'); plt.axis('off'); plt.colorbar();

# 有了一元势函数即可开展对应的推理
# Inference without pair-wise terms
U = unary_from_softmax(probs)  # note: num classes is first dim
d = dcrf.DenseCRF2D(W, H, NLABELS)
d.setUnaryEnergy(U)

# Run inference for 10 iterations
Q_unary = d.inference(10)

# The Q is now the approximate posterior, we can get a MAP estimate using argmax.
map_soln_unary = np.argmax(Q_unary, axis=0)

# Unfortunately, the DenseCRF flattens everything, so get it back into picture form.
map_soln_unary = map_soln_unary.reshape((H,W))

# And let's have a look.
plt.imshow(map_soln_unary); plt.axis('off'); plt.title('MAP Solution without pairwise terms');

NCHAN=1

# Create simple image which will serve as bilateral.
# Note that we put the channel dimension last here,
# but we could also have it be the first dimension and
# just change the `chdim` parameter to `0` further down.
img = np.zeros((H,W,NCHAN), np.uint8)
img[H//3:2*H//3,W//4:3*W//4,:] = 1

plt.imshow(img[:,:,0]); plt.title('Bilateral image'); plt.axis('off'); plt.colorbar();

# Create the pairwise bilateral term from the above image.
# The two `s{dims,chan}` parameters are model hyper-parameters defining
# the strength of the location and image content bilaterals, respectively.
pairwise_energy = create_pairwise_bilateral(sdims=(10,10), schan=(0.01,), img=img, chdim=2)

# pairwise_energy now contains as many dimensions as the DenseCRF has features,
# which in this case is 3: (x,y,channel1)
img_en = pairwise_energy.reshape((-1, H, W))  # Reshape just for plotting
plt.figure(figsize=(15,5))
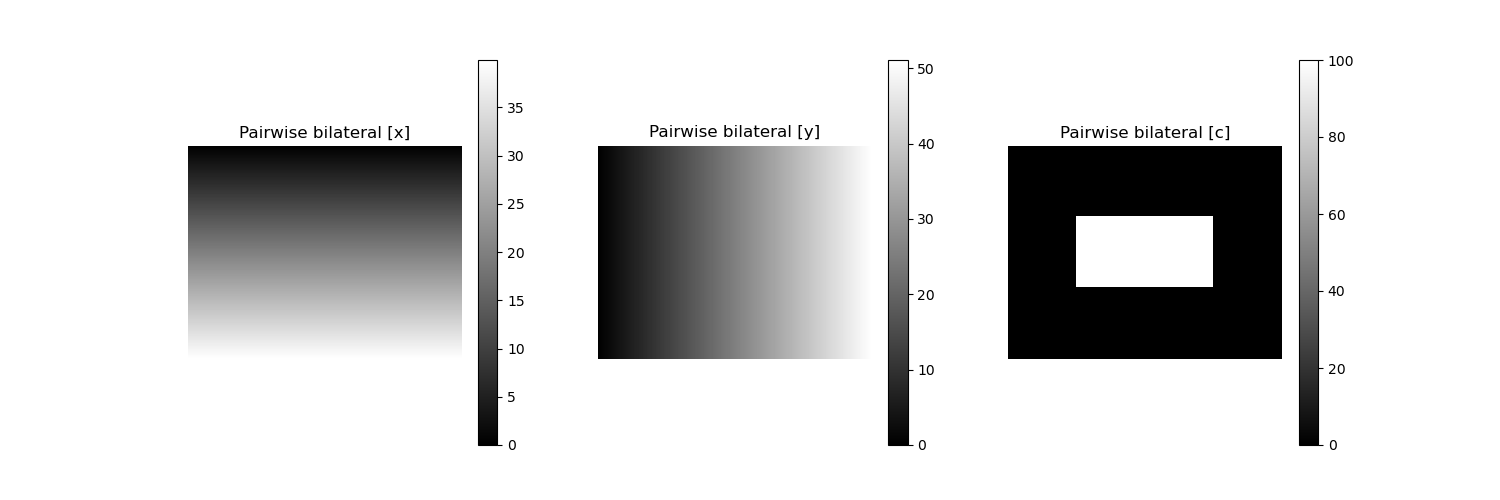
plt.subplot(1,3,1); plt.imshow(img_en[0]); plt.title('Pairwise bilateral [x]'); plt.axis('off'); plt.colorbar();
plt.subplot(1,3,2); plt.imshow(img_en[1]); plt.title('Pairwise bilateral [y]'); plt.axis('off'); plt.colorbar();
plt.subplot(1,3,3); plt.imshow(img_en[2]); plt.title('Pairwise bilateral [c]'); plt.axis('off'); plt.colorbar();

d = dcrf.DenseCRF2D(W, H, NLABELS)
d.setUnaryEnergy(U)
d.addPairwiseEnergy(pairwise_energy, compat=10)  # `compat` is the "strength" of this potential.

# This time, let's do inference in steps ourselves
# so that we can look at intermediate solutions
# as well as monitor KL-divergence, which indicates
# how well we have converged.
# PyDenseCRF also requires us to keep track of two
# temporary buffers it needs for computations.
Q, tmp1, tmp2 = d.startInference()
for _ in range(5):
    d.stepInference(Q, tmp1, tmp2)
kl1 = d.klDivergence(Q) / (H*W)
map_soln1 = np.argmax(Q, axis=0).reshape((H,W))

for _ in range(20):
    d.stepInference(Q, tmp1, tmp2)
kl2 = d.klDivergence(Q) / (H*W)
map_soln2 = np.argmax(Q, axis=0).reshape((H,W))

for _ in range(50):
    d.stepInference(Q, tmp1, tmp2)
kl3 = d.klDivergence(Q) / (H*W)
map_soln3 = np.argmax(Q, axis=0).reshape((H,W))

img_en = pairwise_energy.reshape((-1, H, W))  # Reshape just for plotting
plt.figure(figsize=(15,5))
plt.subplot(1,3,1); plt.imshow(map_soln1);
plt.title('MAP Solution with DenseCRF\n(5 steps, KL={:.2f})'.format(kl1)); plt.axis('off');
plt.subplot(1,3,2); plt.imshow(map_soln2);
plt.title('MAP Solution with DenseCRF\n(20 steps, KL={:.2f})'.format(kl2)); plt.axis('off');
plt.subplot(1,3,3); plt.imshow(map_soln3);
plt.title('MAP Solution with DenseCRF\n(75 steps, KL={:.2f})'.format(kl3)); plt.axis('off');