【现代数学】现代数学入门知识整理（2）

#【现代数学】现代数学入门知识整理（2）

@(现代数学入门)

标签： 【现代数学入门】

一、集合

1. 原像集合与逆映射：这个概念的理解本质上就是逆映射要求为双射，而集合的原像则没有这种要求，这两个不同的概念，逆映射f^-1是映射，而集合的原像f^-1(B)是集合，都使用了f^-1这个符号而已：

   注：(1) f不为单射，由定义，f(A)对应的原像就可能超出A的范围，可以是X-A中的元素，但一定会完全包含A中元素。(2) f不为满射，则B中就可能存在一些元素没有原像，再映射回来的时候B中元素就可能不会完全对应上。

2. 集合的对等：要求为双射，但没有要求为连续。因此，可以在闭区间与R之间建立双射，但是无法建立连续的双射，因为对于连续，开集的原像是开集，闭集的原像为闭集，保持它的闭性。

3. 实数完备性理论：(1)上确界与下确界的定义(大一点点都不再是下界，小一点点都不再是上界); (2)有界实数列存在收敛子列的构造方法（通过闭区间不断分割都能包含A{x_n}无限多项，满足闭区间套定理，收敛，与A作交集，即为收敛子列）; (3)有理数集合中，柯西列未必收敛，典型的例子就是(1+1/n)^n -> e; (4)C[a,b]基本性质，闭区间的连续函数与一致连续是一致的，而开区间则不一样。一致收敛与逐点收敛的区别在于N的选取与x是否有关，一致收敛能够保持函数的连续性。

二、代数结构

1. 群、环、域的基本概念，下图是一个很好地整理说明：内运算与外运算，都是封闭的A×A->A, K×A->A；二元运算封闭则为原群，加上满足结合律为半群，加上单位元为幺半群，再加上逆元则为群，加上交换律则为可交换群或者阿贝尔群；群的性质：方程唯一解（逆元的运算）、方幂运算；子群：它是群的一个子集，天生就满足结合律，存在单位元和逆元，只不过要证明它是对这些东西封闭的，它的刻画为ab^-1仍然在子群内；全交换群S_M是指对集合M到自身的所有双射全体，对于映射的复合构成群，如果M为n元集合，M的双射称为n元置换：两种特殊的置换：对换与轮换：任意的置换都可以表示为有限多个不相交的轮换的复合，构造方法如下：任意取一个置换，假设不为I，那么让它反复作用，必会重复，取前面不重复的t个，剩下的n-t继续选定一个不断作用，这些不断迭代就可以得到有限次的轮换；置换可以表示为对换的复合，且分解不唯一，但对换的次数奇偶性一致：证明方法可以构造多元函数f为行列式，对换分解后为(-1)^m * f，也就是分解的长度奇偶性一样。偶置换的全体构成子群，称为交错群，奇置换的全体不是子群，没有单位元；群同构：保持乘法，sigma(xy)=sigma(x)sigma(y),(R,+)->(R,×)，x->e^x，群同构保持单位元和逆映射；[凯莱定理]任意群G都同构于一个变换群Gl：G太抽象，可以研究Gl，称为G的左正则表示群；环同构：双射保持加法和保持乘法；子环的刻画：子环非空，对加法构成加法子群（a-b在子环内），对乘法封闭（a×b在子环内）。证明环的中心为子环，就要验证这三条，另外矩阵Mn(C)是一个环，它定义的有乘法和加法，它的环中心为数量矩阵，即单位阵×K；向量空间对加法构成可交换群，但向量空间没有定义乘法，内运算只有加法，外运算为数乘。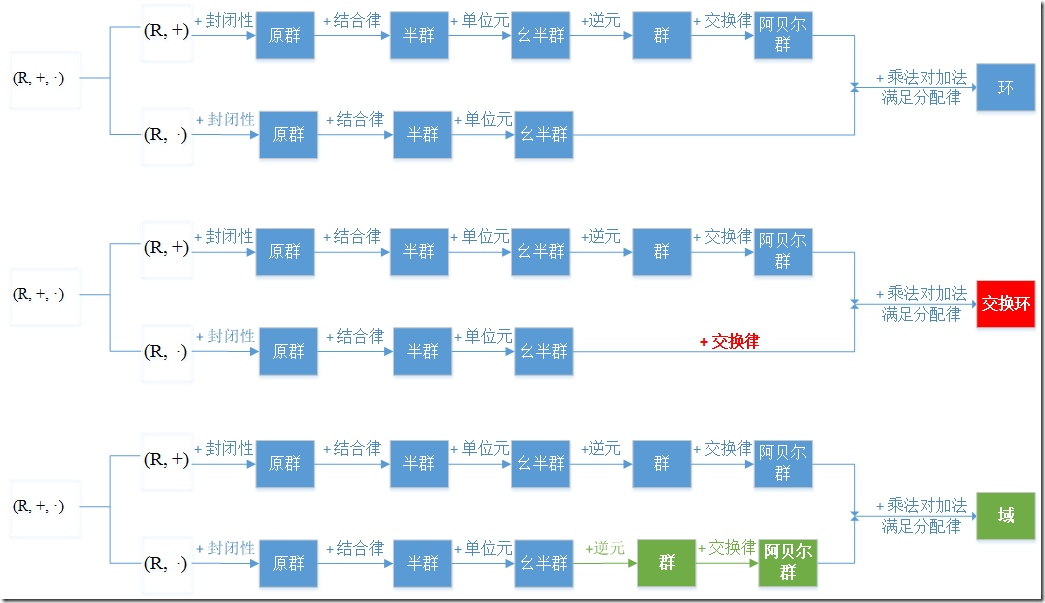

   http://sparkandshine.net/algebraic-structure-primer-group-ring-field-vector-space/

三、勒贝格测度与积分

1. 外测度定义：开区间覆盖的区间长度和的下确界；在证明有理数集合测度为0时，可以将有理数可列列出来，然后构造一列开区间覆盖，开区间长度为epsilon/2^n，这样加起来为epsilon；外测度的性质：单调、次可列可加性和平移不变性；勒贝格内测度=外测度=勒贝格测度，m(E)，勒贝格可测集合的全体为花m；卡拉里奥多利条件用可测集去切割任意的T属于R都能将其满足可加性；对于勒贝格测度则满足不相交集合有可列可加性、花m属于sigma-代数，对于补运算封闭，可列并封闭；还有一个几乎处处的概念就是除了在A的零测集外，都成立，则称之为几乎处处成立。

2. 勒贝格可测函数：定义为可测集合E中x使得f(x)>任意实数a的x的集合,核心理解就是对于任意的a，E(f>a):={x属于E:f(x)>a}，这个集合只要是勒贝格可测集合就可以了。而且勒贝格可测集合花m是sigma-代数。E(f≥a)=可列交E(f>a-1/n)属于可测集合，均为可测函数的等价刻画。开集E上的连续函数是可测函数，可测集合上的连续函数是可测函数，但可测函数不一定连续，比如闭区间[0,1]上的dirichlet函数，有理数的时候为1，无理数的时候为0，处处不连续，但是可测函数。有界可测集合E包含于R上的单调函数是可测函数；可测函数m(E)对四则运算封闭，对可测函数列的上确界、下确界、上极限和下极限都封闭，具有良好的封闭性。大多数可以通过组合进行变换得到证明它是可测函数。

3. 勒贝格积分：就是利用可测函数的定义，对可测集合进行可测分划，有界可测函数，任意分划求和，S(D, f)和s(D,f)，S的下确界和s的上确界，相等时称之f在E上勒贝格可积，E上勒贝格可积函数全体是L(E); 用来证明f属于L(E)的方法可以紧跟定义，比如证明对于任意的epsilon>0, 存在E的可测分划使得S(D, f)-s(D,f)<epsilon，其充分性可以使用夹逼准则来证明，而其必要性就可以构造两个分划，这两个分划一个对应上积分，一个对应下积分，通过任意相交两个分划，构造更细的分划，夹在两个中间，则满足这个条件；大和不增，下和不减；f为有界可测函数，若m(E)<无穷，则f属于L(E);

   对于勒贝格积分与黎曼积分，黎曼积分是直接对x进行分割，而勒贝格积分定义了可测函数，通过函数f映射到R上来对y进行分割，然后对应到x上，因为x是可测集合，概念就得到了推广。

闭区间的狄利克雷函数就是黎曼不可积而勒贝格可积的函数； 而闭区间上的黎曼可积函数，对应为勒贝格也可积，且积分相等；

勒贝格积分的性质：积分单调性，L(E)是线性空间；互不相交的可测集合或者可测分划是可列可加的；如果可测集合E上的两个有界可测函数f,g仅仅在零测集合上不等，那么勒贝格积分是相等的；非负有界可测函数勒贝格积分为0，则函数几乎处处为0

无界函数的勒贝格积分：引入截断函数（f(x)>t的时候让它等于t），截断函数是可测函数，则定义f在E上的勒贝格积分为截断函数的勒贝格积分的极限小于无穷，则无界函数f可积，属于L(E)

对于一般的无界可测函数，定义其勒贝格积分为：如果$f_+$与$f__$为其正部和负部，属于L(E)，则f可积。

四、度量空间

1. 度量空间的基本概念：

   例子：C[a,b]为闭区间上的连续函数全体，定义的度量为d(x,y)=max |x(t)-y(t)| t in [a, b]，C[a,b]构成度量空间；C[a,b]上函数列xn依度量收敛等价于一致收敛；距离是二元连续函数；有界集合被包在一个开球内；有限集合必然是有界的；有界集合的直径有限；有限多个有界集合的并集是有界集合；离散度量空间中任意集合都是有界集合；度量空间中的收敛点列是有界集合（证明是前面N项个个击破，n>N时，定义一个开球的半径为epsilon即可，然后取这N项最大的d作为开球的半径即可得证）

2. 度量空间的点集：

   x0属于A的导集 == 定义 == A-{x0}中存在点列收敛至x0; x0属于A的闭包 == 定义 == A中存在点列收敛至x0 == d(x,A)=0；即点x0到A的距离为0。 连续映射：开集的原像是开集，闭集的原像是闭集，足够小的开球映射到任意小的开球上；正常函数连续的定义； 开映射与连续映射的区别：开映射指的是X中的开集A，像集f(A)是Y中的开集；可逆映射是连续映射的充要条件是f^-1为开映射，也就得到了开集的原像是开集了的概念。

3. 完备度量空间：

   在实数空间中，柯西列是收敛列，但对于一般地度量空间则未必收敛，以度量空间中的柯西列是否收敛为准则，可将度量空间分为完备度量空间和不完备的；完备度量空间中柯西列都收敛；

4. 压缩映射原理：

   压缩映射定理是闭区间套定理的直接推广，压缩映射一定是连续的，如果a=0，则X被映射为单点集；常数a与x,y的选取无关；关键在于构造迭代序列，证明方程有解的条件（线性方程组的行和判别法和列和判别法）；要求完备的度量空间；

五、拓扑空间

1. 拓扑空间的基本概念

   拓扑空间$(X,τ)$：$τ$是X的拓扑，是X的幂集的子集，满足有限交、任意并；由度量空间诱导的拓扑：度量空间中的开集（每个点都是内点）的全体构成一个拓扑空间，如果度量空间不同的度量下诱导的拓扑空间相同，则称之为等价的度量，譬如：l1,l2,l无穷，它们时同样的拓扑，形变连续，保持开集，相近的点还是相近的；离散度量空间任意点都是开集，诱导离散拓扑，离散拓扑可以定义度量，构成离散度量空间；邻域的概念：开球概念的自然延伸，X中的子集U，若τ中存在一个元素V，使得x属于V而V包含于U中，则称U是x的邻域；拓扑空间聚点：A中除了x之外与x的邻域交集不为空；闭集的概念：开集的补集或者包含所有聚点的集合；离散拓扑空间X中的子集都是既开又闭的集合；平庸拓扑空间X的子集中仅有X或者空集为开集。

2. 连续映射与拓扑同胚

   连续映射：f(x)的任意邻域的原像都在x的邻域中；任意开集的原像为开集；任意闭集的原像为闭集；两个映射都连续，复合映射也连续

拓扑同胚：双射，f和f^-1都是连续映射，则称f为拓扑同胚。大致理解就是可以连续变化回来。同胚保持开集；

拓扑空间的序列：拓扑空间点列收敛：存在自然数N使得当k大于N时，xk属于x的任意邻域，则称xk收敛于x；点列的子序列也同样收敛到x；对于平庸拓扑空间，任意的x都是点列的极限；离散拓扑中点点互异的序列极限不存在；与度量空间类似，拓扑空间中集合A属于X，A中除去x的点列xn如果收敛到x, 则x为聚点；f在x点连续，则对于任意收敛到x的序列xn，有f(xn)收敛至f(x).

六、Banach空间和Hilbert空间

1. 赋范线性空间：

   线性空间的代数结构：定义了加法运算的内运算，关于加法构成加法群；定义了数乘运算；数乘关于加法满足分配律；即为向量空间；

赋范线性空间：非负一元函数满足正定性、齐次性和三角不等式称之为范数|| ||；可以将用范数定义度量，从而诱导度量空间；但度量空间不一定是赋范线性空间：比如离散度量空间不是线性空间，度量不满足齐次性等等；C[a,b]上定义的max |f(x)| x in [a,b]、lp范数（注意度量空间中对应的是二元函数，可以有这里的范数诱导出来距离，构成对应的度量空间）、l无穷范数；L(E)上的L^p(E)；依范数收敛与依度量收敛是类似的；范数是一元连续函数，度量是二元连续函数；收敛点列是有界点列；

1. Banach空间：

   Banach空间：赋范线性空间由范数诱导距离，构建度量空间，完备的赋范线性空间就是Banach空间。R^n上的lp范数构成Banach空间；C[a,b]是Banach空间；

Banach空间的两个重要例子：lp空间与Lp空间：lp实际上就是分量按照对应的p次方求和再开p次方；需要验证是赋范线性空间+完备性，是一个范数需要验证正定性、齐次性以及三角不等式，通过Minkowski不等式可以证明满足三角不等式，而完备性证明则通过构造柯西列，然后然后查看每一个分量都为柯西数列，由实数完备性知分量收敛至X=(x1,x2, ...)，再验证X属于lp同时Xk收敛至X即可，考察上面定义的柯西列，在k,l大于N时，小于epsilon，写出前r项，级数求和，首先得让l趋于无穷，分量收敛于xn，然后再令r趋于无穷即可。；Lp空间：勒贝格可测积分，其实等效于lp的连续形式；lp空间是特殊的Lp空间；还有勒贝格积分形式的明可夫斯基不等式；

1. 内积空间和Hilbert空间：

   内积空间定义：赋范线性空间中不存在角度概念，无法定义向量夹角，无法定义垂直的概念，且赋范线性空间的距离不一定满足平行四边形法则；共轭双线性型：二元函数a(·,·)，对第一变元线性，对第二变元共轭线性；共轭双线性型a(·,·)诱导二次型为一元函数q(·);q(x)属于实数R的充分必要条件是a(x,y)与a(y,x)共轭；X上的共轭双线性型为内积，如果满足(1)共轭对称：(x,y)与(y,x)共轭对称，以确保(x,x)属于R，(2)正定性；具有内积的线性空间是内积空间；l2和L2是内积空间，其余lp和Lp不是内积空间，不满足平行四边形法则；内积可以诱导范数，内积空间就是赋范线性空间；范数不一定满足平行四边形法则，当满足时可构成内积空间；完备的内积空间是Hilbert空间，L2[a,b]和l2等势Hilbert空间；内积是二元连续函数；距离是二元连续函数；范数是一元连续函数；。

2. Hilbert空间的正交规范基：

   内积空间中定义的向量x,y正交：(x,y)=0；M是X的子集，M的垂直定义为与M中任意的元素都正交的X中的元素的集合；零向量与任意元素都正交；M与M的垂直交集只有零元素；

正交的基本性质：x与yi正交，那么x与yi的线性包正交；正交满足勾股定理；x与yn正交，yn有极限，则x与yn的极限也正交；M的垂直是闭子空间（封闭的）；M的闭包的垂直等于M的垂直；

内积空间的正交集，标准正交集和完全的标准正交集：正交集中两两相互垂直；标准：模为1；完全：S的垂直为{零元素}；有限维的希尔伯特空间一定存在完全的正交规范集合：可以借助Gram-Schmidt正交化过程来获得：{xn}为希尔伯特空间一组线性无关向量，则存在正交规范集S={en}。y1=x1, e1=y1/||y1||; y2=x2-(x2,e1)e1, e2=y2/||y2||；就这样迭代下去即可。对于无限维的希尔伯特空间借助Zorn引理进行证明，将无限转换为有限；希尔伯特空间完全的正交规范集不唯一，但集合的势是固定的；

内积空间的正交规范基：对于任意的x属于X，$x=\Sigma_{\alpha \in I}(x, e_{\alpha})e_{\alpha}$，$(x, e_{\alpha})$为关于$e_{\alpha}$的傅里叶系数，上述式子是x关于{e_α: α属于Index集合}的傅里叶展开式

H为希尔伯特空间，H上的正交规范集S，S为正交规范基==S为完全的正交规范集合==Parseval等式成立；希尔伯特空间的标准正交基未必唯一；比如l2空间中的坐标系的单位向量就是一组标准正交基；

Hilbert空间同构：线性满射保持内积则称X1和X2为希尔伯特空间同构

1. 内积空间的最佳逼近：

   最佳逼近就是距离上的：指的是在赋范线性空间X上的一点，求该点到X的子空间M的距离：点到闭子空间的距离转化为两点之间的距离。

对于Banach空间点到子空间的距离不能转化为两点之间的距离；而希尔伯特空间，由于有垂直的概念，点到闭子空间的距离可以转化为两点之间的距离。最佳逼近点存在，且唯一，最佳逼近点就是垂足，垂足就是最佳逼近点

正交分解定理：H是希尔伯特空间，M是H的闭线性子空间，对于H中任意的元素x，存在唯一的分解：x=y+z，y属于M，z属于M的垂直。投影算子：$x0=Px,P: H\rightarrow M$为映射；

正交分解定理应用于给定函数$f\in L^2[a,b]$，要求用给定的函数$f_1,f_2,f_3,…,f_n$线性组合按照平方平均意义求最佳逼近。从分析学上看，就是求x到M的最佳逼近点；从几何上看，就是求x在空间$M=span{x_1, x_2, …, x_n}$上的正交投影。如果恰好${x_1, x_2, …, x_n}$是一组正交规范集，那么投影系数就是傅里叶展开系数：$(x,x_i)$，一个案例就是$f(x)=e^x$, 求区间[0,1]上均方逼近它的最佳二次多项式，一种简单的解法就是求二次多项式空间的标准正交基，然后计算傅里叶展开系数即可。

七、线性有界算子与线性有界泛函

1. 线性有界算子：

   线性空间的线性算子：线性空间映射A：X->Y，任意满足A(αx+βy)=αA(x)+βA(y)，若Y为R(C)则为线性泛函；线性算子将零向量映射为零向量；$ker A ={x\in X: Ax=θ}$为X的线性子空间，核空间，其中求导运算、积分运算和核积分算子；

线性算子的有界性和连续性：赋范线性空间的连续性定义没差，x->x0，Tx->Tx0，一个非常有意思的区别是线性算子T连续当且仅当在零点连续或者在某一点连续，T有界；赋范线性空间的线性算子T有界，当且仅当T将有界结合映射为有界集合；有界就是存在一个C>0，不依赖于x的选取，有Tx的模小于等于C乘以x的模；还等价于拓扑空间中连续的刻画：开集的原像是开集，闭集的原像是闭集；

线性有界算子空间： 更进一步地，如何构造一个线性有界算子空间呢？

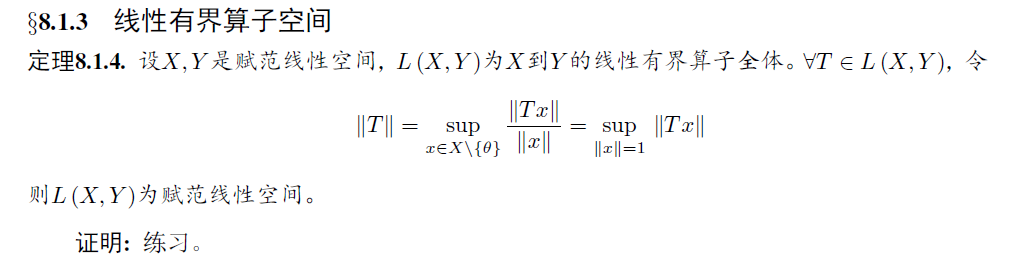紧扣定义：赋范线性空间，有界线性算子，上确界。

证明很简单，从定义出发，齐次性与正定性显然满足，而三角不等式，从这个定义的T的范数就可以带入进去计算，从X，Y的赋范线性空间属性的三角不等式可以推出这里的三角不等式。

有两个比较重要的说明：||T||为上确界，而有界算子则表现为||Tx||<=C||x||，C的下确界就是||T||。

所以可以通过这个取得到的方式来证明C或者||T||是等于某一个值的。

关于算子，其实就是要把它的作用方式写出来，然后各自求范数，判断其大小关系，从而找出一个合适的确界。 对于L(X,Y)是Banach空间，只需要Y是Banach空间即可； 正交投影算子P的范数小于等于1（x=Px+y正交分解定理：||Px||=||x||^2-||y||^2<||x||^2），当M不为空集时，P的模为1, 取上界，将Px0=x0.。

赋范线性空间上的线性有界泛函全体构成Banach空间x*为X的共轭空间;l2是自共轭空间，p和q是共轭空间； 赋范线性空间的弱收敛是在任意的线性泛函f,f(x_n)->f(x)；有限维NLP弱=强；

1. Riesz表示定理：

   希尔伯特空间的共轭空间：收敛与弱收敛，与赋范线性空间的弱收敛定义不同，其实也不能称之为不同，而是其特例，线性泛函可以由内积来定义，所以，希尔伯特空间的弱收敛定义为xn对任意的y的内积极限等于x与y的内积，xn弱收敛于x。

H*中的任何元素都可以唯一的写成内积的形式：(x, x_f)，而这个x_f是唯一的；

2019-01-10 17:00 张朋艺

2019-01-11 13:29 张朋艺