【计算机视觉】Fast High-Dimensional Filtering Using the Permutohedral Lattice
大一统的高维高斯滤波表达式

对任意的位置 pi 处的值 vi 进行滤波,与具有临近位置的其它值进行混合。通常这些值 vi 是均匀的像素颜色。
- 如果位置
pi是两维的像素位置,那么该公式表达的是高斯模糊Gaussian blur。 - 如果位置
pi是像素位置与颜色的联合,比如x,y,r,g,b共五维,那么该公式表达的是颜色双边滤波color bilateral filter。 - 如果位置矢量
pi是来自每个像素的局部邻域,那么该公式表达的是非局部均值no-local means。
关于多维度高斯滤波的发展
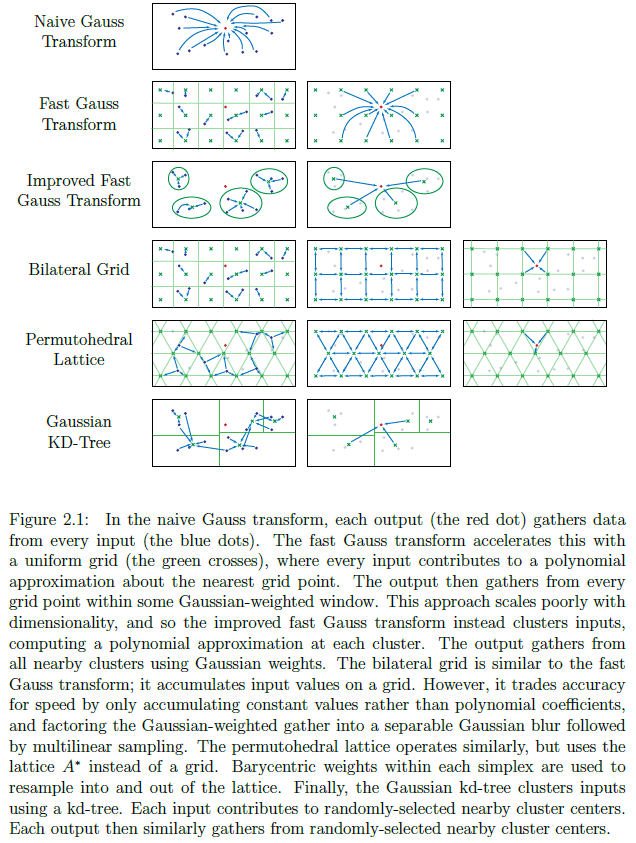
-
朴素高斯转换
Naive Guass Transform:每个输出从每一个输入获取数据,就是单纯的所有输入的加权平均; -
快速高斯转换
Fast Gauss Transform:用一个统一的网络加速,每个输入给这个最近的网格点贡献一个多项式的近似值。然后输出则从在一些高斯加权的窗口内的每个网格点上获取数据。这种方法当维度高的时候就不太灵了; -
改进的快速高斯转换
improved Fast Gauss Transform:不再划分网格,而是对输入进行聚类,然后对每个聚类计算一个多项式近似。然后输出则从所有临近的类簇中搜集数据高斯加权; -
双边滤波
Bilateral Filter:与快速高斯转换相似,将输入值累计在一个网格中,然而它用精度换速度的方式只累计常数项而不是多项式系数,将高斯加权的集合分解为分别的高斯模糊,之后进行多线性采样; -
Permutohedral Lattice:相似地,不过使用的是晶格A*lattice而不是一个网格grid,在每个单形simplex内的重心权重被用来重采样到晶格和重采样出晶格。 -
高斯kd树
Gaussian kd-tree:使用k-d树对输入进行聚类,每个输入给随机选择的临近的聚类中心贡献,而每个输出则相似的从随机选择的临近的聚类中心收集。
本文介绍的方法是使用 Permutohedral Lattice 进行快速高维度滤波。
Permutohedral Lattice
一个Toy说明 Splat-Blur-Slice pipeline
其实跟 bilateral filter 的pipeline相类。所以,首先先介绍一个更加简易的一维的 Splat-Blur-Slice pipeline 如下所示:
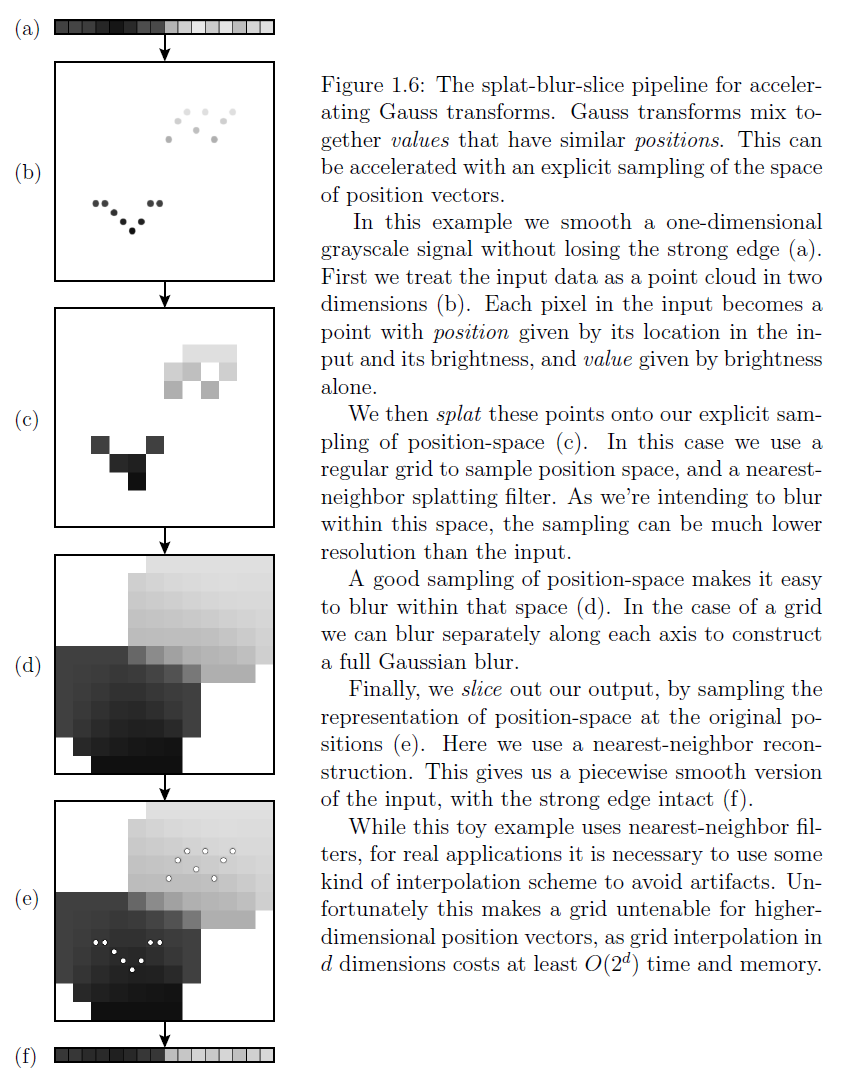
将输入的一维数据当做两维的点云;在输入中每个像素变成了一个点,这个点具有由其在输入中位置和其亮度所给定的 position 以及由亮度单独给定的 value。 然后将这些点 splat 到位置-空间的显式采样上。我们可以用一个规则网格来采样位置空间,使用最近邻 splatting 滤波器。由于我们想在这个空间进行 blur,这个采样可以比输入的分辨率更相当低一些。一个好的位置-空间采样使的在这个空间进行 blur 容易,在一个网格的情况下,可以分别沿着每个轴单独 blur 来构建一个完整的 Gaussian blur。最后, slice :通过在原始位置采样 位置-空间 的表示来得到输出。这里直接采用最近邻重建。可以给出输入的分段光滑版本,具有良好的强边缘保持作用。这个示例版本直接采用了最近邻的滤波器,在实际应用中有必要使用一些内插机制来避免伪影。不幸的是,对于更高维度的位置矢量,制作网格不太可持续,因为在d-维的网格内插需要至少 O(2^d) 时间和内存。
Permutohedral Lattice
下面看看采用这种 Permutohedral Lattice 方式如何进行:

-
使用超平面
Hd的正交基,将位置d维的位置矢量pi嵌入到其超平面Hd中; -
使用重心的权重,将每个输入值
splat到它所属的simplex单形上; -
栅格点使用可分离的滤波器和临近栅格点来
blur;以图示为例,在三个方向上分别进行分离的卷积,等效直接一个大的卷积。 -
slice:使用相同的重心权重在每个输入位置内插得到输出值。
下面稍微介绍一下几个基本概念,用以理解这么做的好处:
d-维的 Permutohedral Lattice 晶格

首先从一个 d+1维度的离散grid网格出发,将其投影到一个超平面上: x*(1,1,1,...,1)=0。晶格点具有的坐标分量每个都可以被(d+1)取余后余数相等。相应的晶格点被描述为 remainder-k point。晶格将空间镶嵌为一致的单形 simplices,每个 simplex 都具有每种余数 reminder 的顶点。这些单形是标准单形的平移和置换 (现代数学集合论中的平移与置换),可以被不等式所定义。
具体更多的数学,不再介绍了。总之,这个它有以下几条属性:
1. Permutohedral Lattice 晶格将空间镶嵌为一致的单形
2. 封闭任意点的单形的顶点可以在 O(d^2) 时间计算出来
3. 最近邻的晶格顶点可以在 O(d^2) 时间计算内找到
具体如何使用 Permutohedral Lattice 计算高斯转换
位置矢量嵌入到子空间 Hd
将位置矢量嵌入到 Hd,对于rgb图像,得到5-D的位置矢量 pi=[xi/σs,yi/σs,ri/σc,gi/σc,bi/σc]。σs 为空间标准差,σc 为颜色空间标准差。用期望的标准差的倒数来进行scaling。
使用正交基将位置矢量嵌入到子空间 Hd:

Splatting
当每个位置都被嵌入到超平面,必须识别它所附属于的单形,并计算重心权重。
一堆数学公式飘过…
Blurring
将输入重新取样到晶格上,下一步是 blurring along the lattice。用一个 [1,2,1] 的卷积核沿着每个晶格方向来卷积,每个这样的卷积具有方差 d(d+1)/2,所以这d+1个卷积联合起来的效果是近似总方差d(d+1)(d+1)/2的高斯核。这里忽略尺度scale是因为有一个homogeneous齐次项在,可以实现尺度不变。模糊阶段从每个晶格点传递能量至O(3^d)个neighbors。
Slicing
与splatting等效,只不过是使用重心权重来从晶格点收集,而不是散布它们。
算法流程

Enclosing,集合的封闭。
其实整个算法流程还是比较明晰的,只是描述起来,特别是牵扯到集合描述,可能就有点抽象。参照这个算法去理解对应的实现可能会把握的更加清楚。
C++ code
https://github.com/MiguelMonteiro/permutohedral_lattice
论文参考
20200411