【计算机视觉】图像分割之图割

max-flow 与 min-cut

min-cut

一个最简单的例子就是从原点 S (source) 到目标点 T (sink) 有三条路径，每条路径都有一个代价 c (cost)，最小割的意思就是切断 原点 S (source) 到目标点 T (sink) 的通路，且保证所减掉的边的代价之和最小：

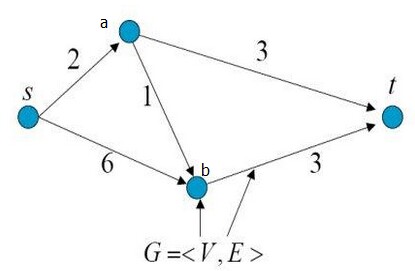
很明显s->a以及b->t这两个边砍断代价最小。正所谓min-cut

max-flow

S能流入T的最大流量，边想象成管道，权重表示流量，那么T点能够流入的最大流量是 2 + 3 = 5，而起到约束作用的边就是s->a以及b->t这两个edges。此所谓最大流。

可以看到，最大流和最小割结果一致，其实不奇怪，福特-富克森定理表明这两者是等价的。而一般最小割问题也会转化为最大流问题进行求解。

Graph-cut图割

Graph cuts是一种十分有用和流行的能量优化算法，在计算机视觉领域普遍应用于前背景分割（Image segmentation）、立体视觉（stereo vision）、抠图（Image matting）等。

图像可以表示为一张无向图，G(V,E)，V是顶点集合，E是边集合。在Graph Cut中这个图多了两个顶点，一个是源点S，一个是汇点T。每个像素顶点跟这两个顶点都有连接，构建为t-links的边。

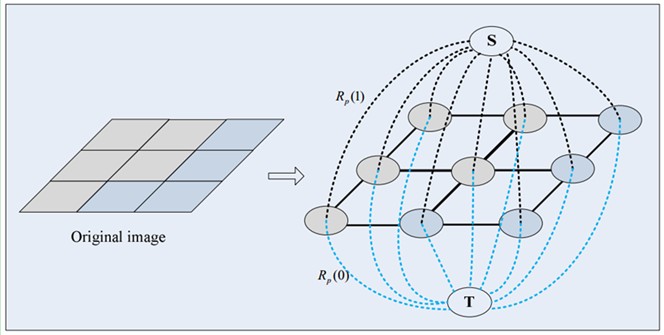
t-links与n-links

一般前景、背景分各种，S表示前景目标，T表示背景，每个像素点与S/T相连的边为t-links，而像素之间只有四邻域的连接，叫做n-links。

Cuts

Cuts是一组边的集合，这些边的断开会使得S->T没有通路，也就是将每个像素只与S或T中的一个相连接，t-links断裂实现分类，实现前景和背景的分离，而对应n-links断裂则是空间上的边界断裂。

跟上面介绍的最小割一样，这样的Cuts对应的权重或者代价之和最小。

权值与代价 costs

如何确定这些costs呢？根据具体前景与背景的分割任务，可以想象，前景与背景是有一些外观差异的，最直接表现在像素值的差异性。那么t-links对应的代价可以是像素值与目标像素或者背景像素的相似度，相似度越大，对应的切割代价就应该也大。那么n-links对应的代价又该如何确定呢？邻域连接，属于同一目标的像素会有邻域相似性，而相似性比较差的区域往往是前景与背景的交界处。这种度量正好拿来作为n-links的权重。如果邻域内相连的两个像素像素值相近，那么断开该link的代价就应该高。

基于上面这样简单的逻辑，可以设计如下的代价函数：一元势函数+二元势函数

给定一个Cuts L，也就对应给定了每个像素的标签 L={l1, l2, ..., lp}，li为0 背景和1 前景，此时对应图的能量为：

E(L) = a * R(L) + B(L)

R(L)，区域项，对应为一元势函数，表示断开t-links的代价，B(L)，边界项，对应为二元势函数，表示断开n-links的代价。a表示对应的重要因子，当a=0时表示只考虑断开n-links的代价。

区域项 R(L)

那么R(L)=∑Rp(lp), p ∈ P。Rp(lp)为像素p分配标签lp的代价，可以将像素p的灰度值与给定前景区域的灰度直方图进行比较来计算，即可得到属于lp的概率。一般取概率的负对数。Rp(lp=1) = -ln Pr(lp=1|Obj), 表示给定前景目标的情况下，像素p属于前景目标的概率取负对数。当像素p与前景目标相似，那么将其分成背景的代价就大，而分成前景的代价就小。同样，Rp(lp=0) = -ln Pr(lp=0|bkg)为将像素p分类为背景的代价。概率大，对应的代价就小，这里的代价也可称为图的能量。

边界项 B(L)

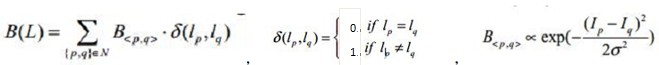
只考虑领域的n-links，对于任意属于领域的p,q，此时这两者之间如果同属一个标签，因为是领域，则没有任何代价，δ函数就是起到这个作用。如果不属于同一个标签，则需要计算对应的两个像素之间的相似度。可以分析，p和q像素值相等，对应的B<p,q>值会比较大，而被分为不同的标签则需要较大的代价。

Graph-cut 示例

Graph cut的3x3图像分割示意图：我们取两个种子点（就是人为的指定分别属于目标和背景的两个像素点），然后我们建立一个图，图中边的粗细表示对应权值的大小，然后找到权值和最小的边的组合，也就是（c）中的cut，即完成了图像分割的功能。

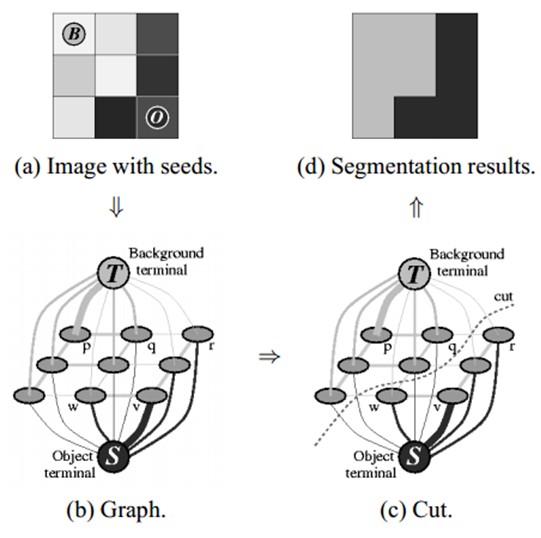
具体实现，可以参考：Medpy graphcut maxflow

2020-04-07